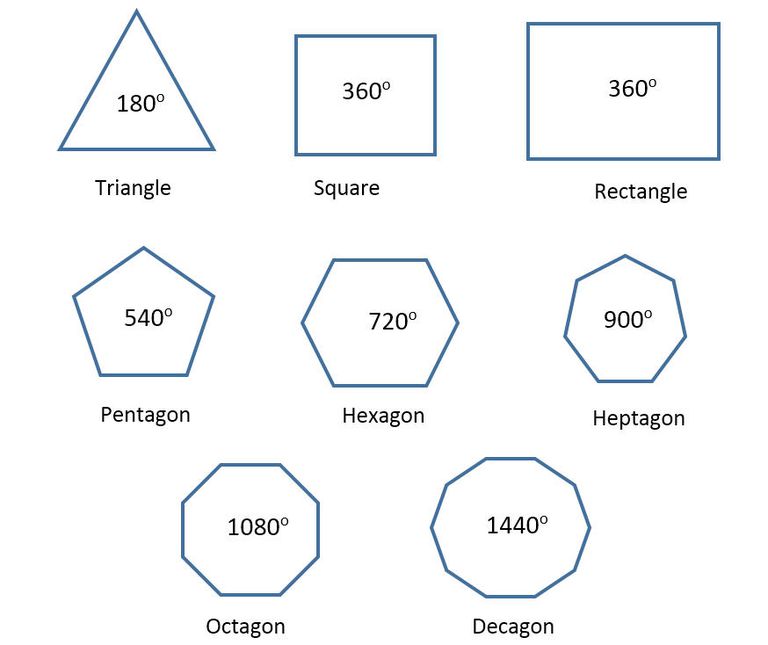
同様に球面上の三角形も,(同一大円上にない)三点を選んでそれぞれを大円の劣弧で結んだものとします。 次に角度についてです。大円どうしの交点の角度を その交点におけるそれぞれの接線のなす角度 で定義します。それを特定するためにとった角度や太陽の角度を測った。 5 1322 50歳代 / エンジニア / 非常に役に立った / 使用目的正多边形是边长相等,角度相同的多边形。 比方说,等边三角形和正方形就是正多边形,美国国防部的五角大楼是一个正五边形,而停车标志是正八边形。 如果是正多边形,只用将内角总和除以角的个数即可。 因此,等边三角形的每个角都是180/3,或60度;正方形的每个角都是360/4,或90度。 (虽然长方形从定义上来说不是正多边形,但它的所有角也都是直角,每个角

正五角星每个锐角度数正五角星的每一个锐角的度数
5角形 角度
5角形 角度-星形五角形の印をつけた 5つの角の和は何度でし ょう。 どんな星形五角形でも印をつけた 5つの角の和は180°になる。そ のりできるだけ多くの方法で説明 してみよう。 こ 今まで習ったことを使えば、 星 形五角 の印をつけた5 つ の角 和は180°になる 3/6 但是,如果我们在做星形的时候,按住ctrl键再绘制星形形状的时候,就可以调出不同的角度了,如图,向外拉伸调节角度,角会变的很小 此文章非法爬取自百度经验 4/6 当我们在按住ctrl键调节角度时,这时候如果再按下alt键,这时候所绘制的星形就会直接生成正规的五角星形状了,如图 5/6 再使用ctrl键做角的时候,向外和向内拓展,会做出不同角度的星形




如何计算角度 8 步骤 包含图片
(1)三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。角の性質や半回転の角度、4直角の角度を求める問題 11人(73%) 4人(27%) 三角形の弁別を問う問題 13人(87%) 2人(13%) 三角定規のそれぞれの角の大きさを求める問題 10人(67%) 5边长为345的三角形面积是多少 : 边长为345的三角形是直角三角形,故直角三角形的面积S=1/2*3*4=6 三边分别为345的三角形,各角度数是多少: 3687°,5313°,90°解答过程如下因为3^24^2=5^2,所以是直角三角形,边长为5的对应角为90°边长为3的对应锐角的正弦值为3/5
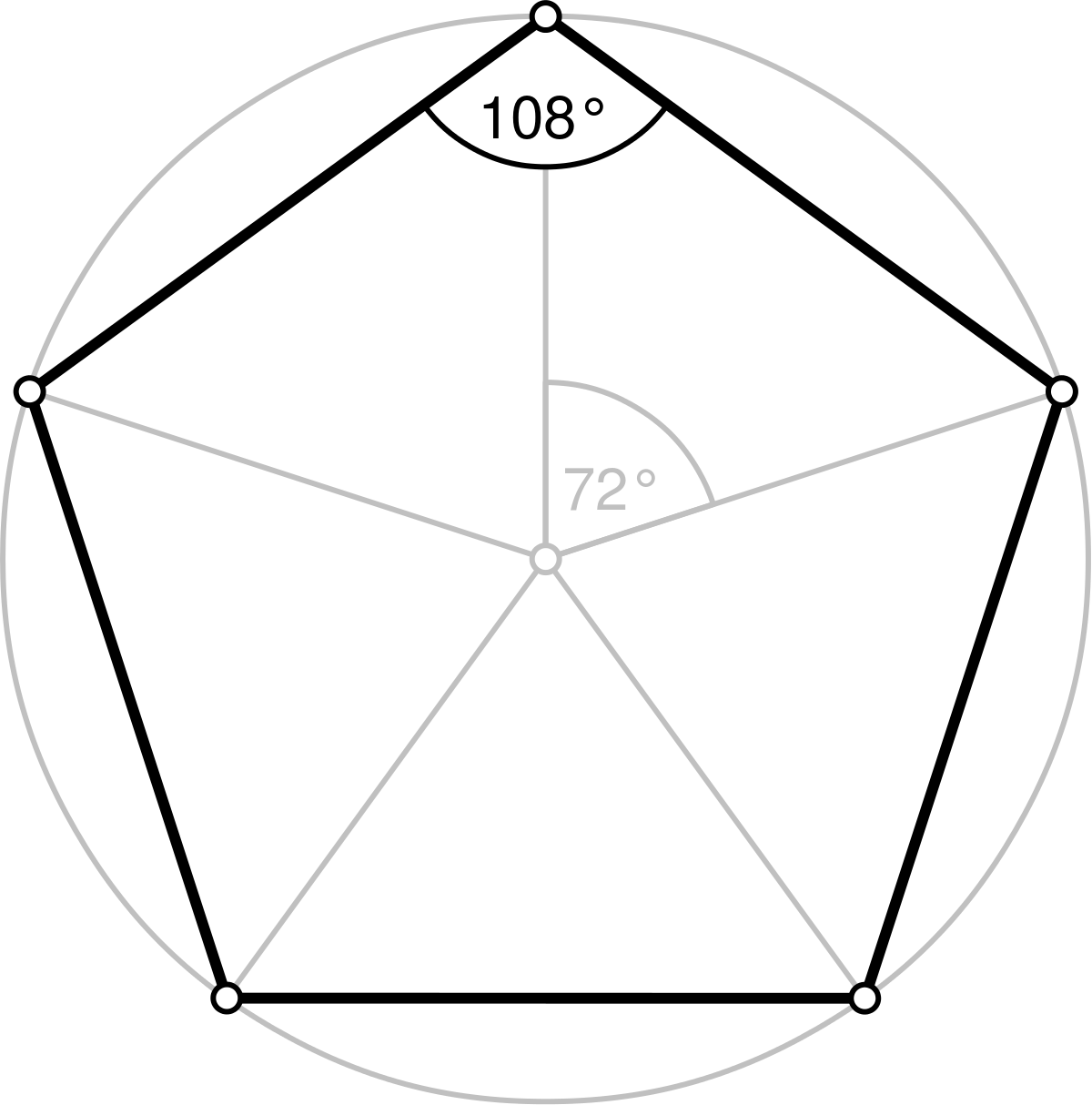
五边形有 5条边,可以由 三个三角形 组成,所以 它的内角的和3是 3 × 180° = 540° 如果是个 正 五边形(所有角度相等),每个角是 540 ° / 5 = 108 ° (练习:确定每个三角形加起来是 180°,五边形加起来是 540°) 今回は、三角形の角度を求める問題を解いていきたいと思います。 三角形の内角の和は180° 三角形の外角の大きさ=となり合わない2つの内角の和 三角形の角度を求める問題 問題① 問題② 問題③ 問題④ 三角形の角度を求める問題では、対頂角・同位角・錯角の性質や二等辺三角形の性質入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 女子校 直角三角形 4年生 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 二等辺三角形 直角二等辺三角形 立体の切断 ファイ
c15 五角形の角の和が540°なので,5で割って108°です。 t でも,どうして5で割ることができるの。 c16 五角形には角が5つあって,一つの角の大きさを知りたいのだから,5で割ることが5年 ジャンプ 1 下の四角形で,ア~エの4つの角の大きさの和は何度になりますか。 また,それはなぜですか。わけを書きましょう。 4つの角の大きさの和は( ) 2 次の図形のアの角度を求めましょう。四角形の4つの角の大きさの和は、 3つの角の大きさの和は( 180゜)(360゜)になります。 30゜ 90゜ 60゜ 90゜ 45゜ 45゜ 分度器を使って,いろ いろな三角形の角度を調 べましょう。 また,三角形をもと に,四角形の4つの角の



多邊形幾何 五角形 六邊形和十二邊形



五角星各顶角之和为 信息阅读欣赏 信息村 K0w0m Com
正五邊形是指五個邊等長且五個角等角的五邊形,其內角為108度,是一種正多邊形,在施萊夫利符號中可以用 {} 來表示。 正五邊形的中心角為72度,其具有五個對稱軸,其旋轉對稱性有5個階(72°、144°、216° 和 2°)。 ミズキ そうそう。中心角とは2本の半径の線がつくる角度のこと。図の ~ の角度のことを中心角と言います。 カイト てことは、360度の5等分が正五角形の中心角の大きさになるんじゃねぇーか? カイト よし、2問目もなんとかクリア。 不规则四边形求角度 l1 2670 l2 2758 cosx h1 713 h2 1371 a 3017 b 2754 角l2\h1 角h1\l1 完整公式 首页 文档 视频 音频 文集 文档




四边形 正方形 长方形 菱形 梯形 平行四边形



江恩六角形中角度线的用法 赢家财富网
这种以"度"作为单位来度量角度单位制叫做角度制。下图是我们常见的180 o 角度尺 Protractor。 2 弧度制(Radian Measure) 长度为半径长的弧,所对的圆心角是 1 弧度(Radian),用符号rad表示。 正角度弧度数是一个正数,负角度弧度数是一个负数,零角度弧度数。正五边形 是指五个边等长且五个角等角的五边形,其 内角 为108度,是一种 正多边形 ,在 施莱夫利符号 中可以用 来表示。 正五边形的中心角为72度,其具有五个对称轴,其 旋转对称性 有5个阶(72°、144°、216° 和 2°)。Sin(x) = 05 我们可以重写为: x = sin1 (05) 我们用计算器来做:输入 05,按 sin1 键,答案便出来了: x = 30°




如何利用编程机器人程小奔编程玩几何 Makeblock



1
已知2直角边,求角度 —— 斜边=(11^2192^2)^05=2213 角1=arc sin(11/2213)=2981度 角2=arc sin(192/2213)=6019度 已知直角三角形两直角边求角度 —— 解用勾股定理计算出斜边 你的斜边长度是对的 斜边≈(米) 不过计算角度时这个斜边是可以不用的 设∠acb=90度,ac=6米,bc=045米 则tan∠a=bc/ac =045/6 =0075小学校5年生で習う「三角形の内角の角度」 を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。印刷してご活用ください。 ちなみに三角形の内角の角度の求め方についてはこちらに詳しく説明しています。三角形の3辺から角度を計算 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 台形型の部屋の変形のコーナーに壁にピッタリと合った棚を作ろうと思い図面を牽きましたが角度の算出方法が分からずお世話になりました、凄く助かり



八十度角的图片 万图壁纸网




十边形 Wikiwand
_____ 因为任意n边形内角和180(n2) n≥3且为自然数 正n边形各内角为180(n2)÷n n≥3且为自然数 原因因为任意n边形外角和总为为360度,一个内角和一个外角和为180度,n边形有n对内角外角,所以有任意n边形内角和180(n2) n≥3且为自然数Sin 18 ∘ = 5 − 1 4 {\displaystyle \sin 18^ {\circ }= {\frac { {\sqrt {5}}1} {4}}} で、これに 黄金比 を掛けると1/2になる。 つまり、2sin18°は黄金比の 逆数 。 五角数 は 多角数 の一つである。 正五角形の1つの頂点からの2本の対角線と1辺とでできる三角形は 黄金三角形 である。 水平な底辺を持つ正五角形の右下の辺の傾きは「高さ×2÷底辺の長さ」となっている。 正小学5年生の算数 多角形の角 三角形の角 問題プリント ツイート 無料ダウンロード・印刷できる、三角形の角度を求める問題プリント です。




0428 多邊形對角線有幾條 Youtube




五边形 维基百科 自由的百科全书
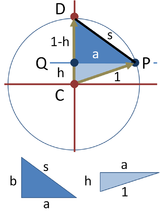
二等辺三角形の角度の求め方 厳選6問解説!←今回の記事 正三角形の角度 正方形、ひし形との融合問題を解説! 平行四辺形とひし形の違いってなに?? 平行四辺形の角度、辺の長さを求める問題を解説这个图形里面出现了以下角度: 18°角: , 36°角(18°的2倍角): 72°角(18°的4倍角): , 90°角(18°的5倍角): , 显然, 是一个等腰三角形,CA=CB。 CO是底边AB的中垂线,OA=OB。 只要我们能算出 的 底边AB 和两腰CA、CB的长度之比,就能立即得出 sin18° 和 sin72°,再利用三角函数的性 弦5相对着的角是90度,勾3的对角是37度,股4的对角为53度。 详细解释:首先由勾3股4弦5知三角形满足勾股定理,是直角三角形;设勾3的对角是A,股4的对角为B。 那么sinA=3/5,A=arcsin3/5=37度。 sinB=4/5,B=arcsin4/5=53度。




初中数学培优八年级下第九讲多边形重高自招题比中考压轴题难 每日头条



角度 五角形 中学から数学だいすき




正多边形 维基百科 自由的百科全书



高雄宅速修室內裝修企業有限公司 高雄水電維修工程




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




微博搜索



知乎日报 知乎




八角形计算公式 八角形有哪些计算公式 三人行教育网 Www 3rxing Org



画像をダウンロード6角形角度 シモネタ




兩種解題方法求五邊形內角和 知識點需要明晰推導過程進而歸納 每日頭條



初中数学 梯形的五种常用辅助线添加方法 17道例题详解培优几何 雪花新闻




簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく
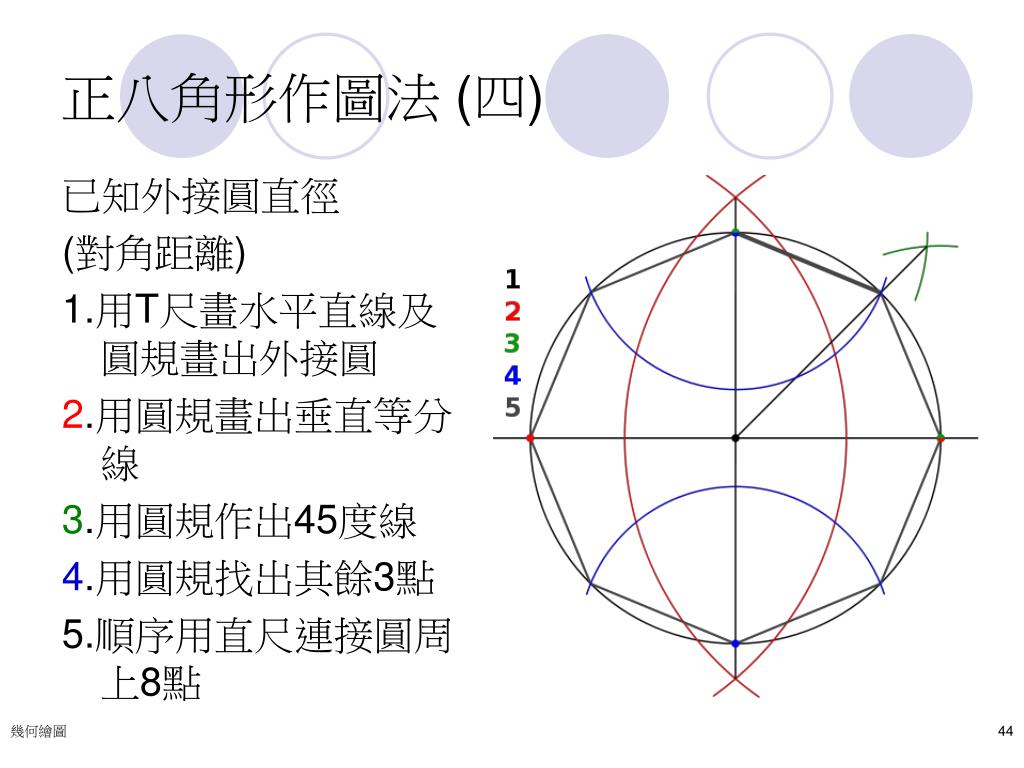



Ppt 幾何繪圖g Eometrical Drawing Powerpoint Presentation Free Download Id




5角形角度 シモネタ




六边形网格 探索者专栏 Csdn博客 六边形网格
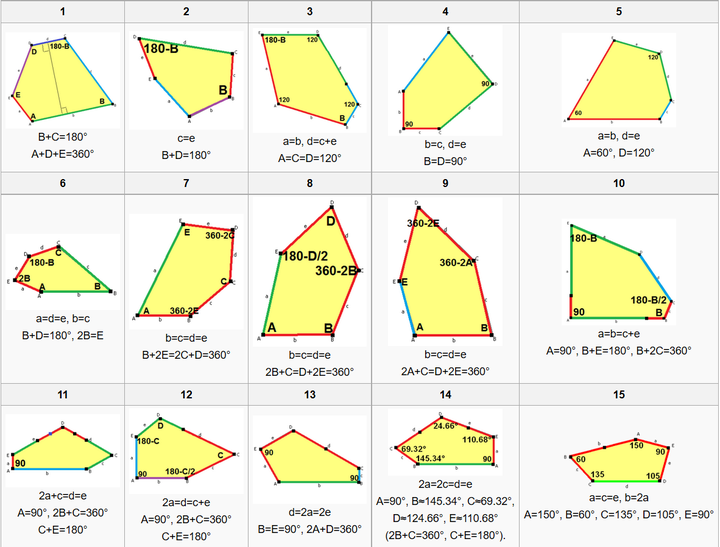



5角形角度 シモネタ




正多边形 属性



初中数学几何 梯形辅助线 的做法详解 孩子成绩提升分




如何计算角度 8 步骤 包含图片




多角形の内角の和 外角の和の公式 数学fun




3种方法来求三角形的第三个角




303 8多角形求法與畫法 拙園創意木工 隨意窩xuite日誌




兩種解題方法求五邊形內角和 知識點需要明晰推導過程進而歸納 每日頭條




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



角度 五角形 中学から数学だいすき
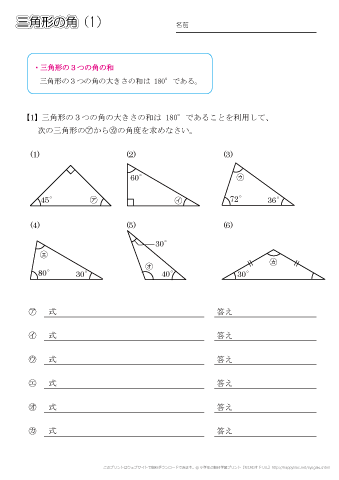



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生



等角五边形中每个角度的大小是多少 等角六角形 教育小本子




如何计算角度 8 步骤 包含图片



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス




八边形 Wikiwand




如何计算角度 8 步骤 包含图片



江恩六角形的结构 赢家财富网




小学5年生 正多角形 算数 Active Learning 学院




六边形网格 探索者专栏 Csdn博客 六边形网格



六角形五角形英文六角形的中的英文 中文 英文字典 格洛斯貝 Doreff




如何 多边形几何 五边形 六边形和十二边形 21




十边形 Wikiwand




國中生常考的正五邊形角度問題 Youtube




正五角星每个锐角度数正五角星的每一个锐角的度数




画一个半径为2cm的正五边形 再作出正五边形的各个对角线 画出一个五角星 雨露学习互助




5角形角度 シモネタ
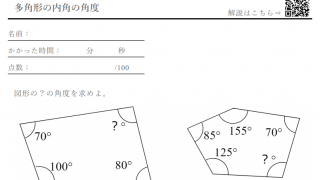



多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




正五边形计算器




多角形の内角の和 は何度なのか を説明します おかわりドリル



悟空问答 五边形内角和是多少 个回答
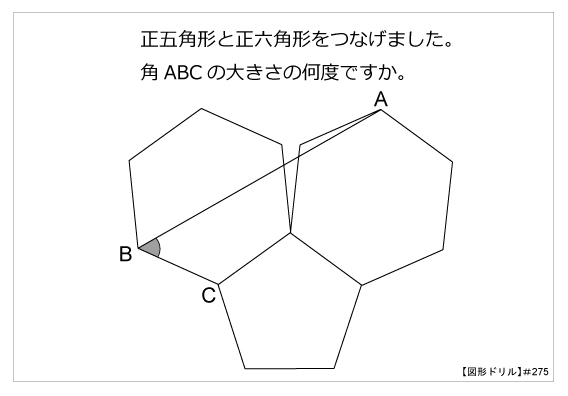



図形ドリル 第275問 正五角形と正六角形 算数星人のweb問題集 中学受験算数の問題に挑戦




N邊形內角和定理 Youtube



初中数学 梯形的五种常用辅助线添加方法 17道例题详解培优几何 雪花新闻




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




圆内接多边形 维基百科 自由的百科全书



1




多边形的内角
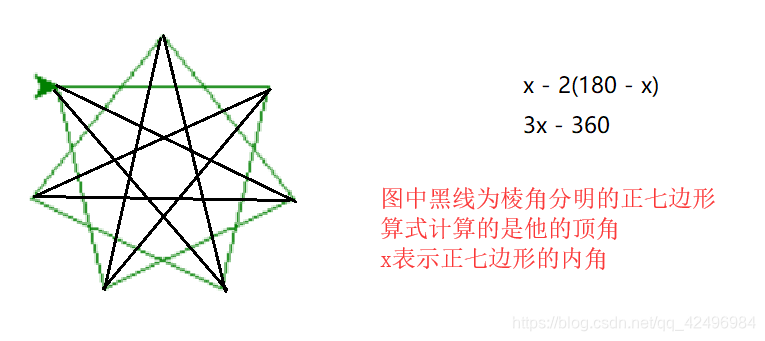



Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 Turtle画多边形



五边形 维基百科 自由的百科全书
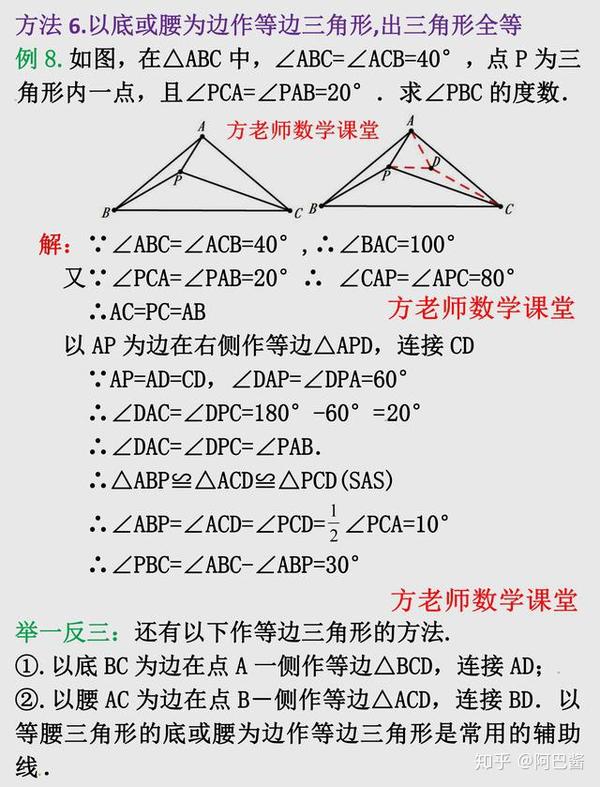



初中数学 等腰三角形 7种常用辅助线的添加方法 技巧归纳专题 知乎




3种方法来求五边形的面积




正五邊形怎麼畫 Youtube




多邊形之五邊形內角和計算 Youtube




正五角星每个锐角度数正五角星的每一个锐角的度数
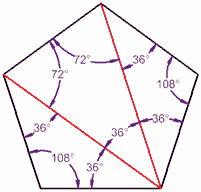



多边形的内角




例題 五邊形的五個角度比 Youtube




七边形 Wikiwand
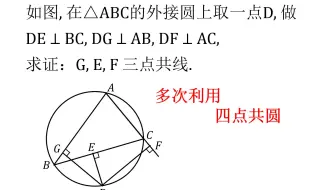



初中数学 五角星5个角是多少度 你会吗 哔哩哔哩 Bilibili



初中数学几何 梯形辅助线 的做法详解 孩子成绩提升分



剪紙教程 七種基本剪制方法 雪花新闻
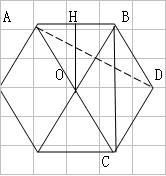



六边形一定有六条边六个角




小学校5年 算数 正多角形の角の大きさ Youtube



九边形 Wikiwand
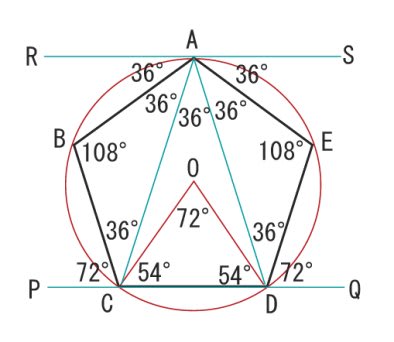



上6 角形五角形角度 シモネタ



五角星与等腰三角形 1 4角平分线的性质 初中湘教版13版 数学中国网
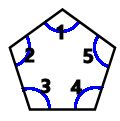



正五角形の内角 外角




3种方法来画六边形



知乎日报 知乎



什么是江恩六角形 赢家财富网




慧话 连篇 5 8角形角度




程序计算五角形三角形个数 Word文档在线阅读与下载 无忧文档



八边形的对角线是什么 教育小本子



五边形 维基百科 自由的百科全书
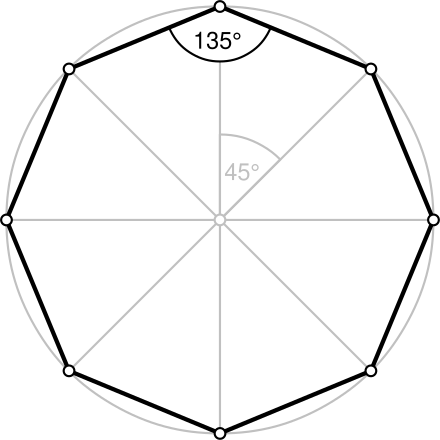



八边形 Wikiwand




圆内接多边形 维基百科 自由的百科全书




画像をダウンロード6角形角度 シモネタ



1




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




五角星外角和怎么求 五角星的内角和还有五角星的外角和怎么求 三人行教育网 Www 3rxing Org



1



下面的人如何解决这个数学问题 教育小本子




十一边形 Wikiwand



五边形 维基百科 自由的百科全书
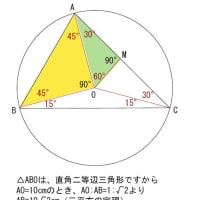



正五角形というだけで 分かる角度は 名寄 算数数学教室より



五邊形求角度 四邊相等 已知三角 求剩餘角 Hk 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩




计算六角形的面积 建议 July 21




多边形的内角




五边形中有几个三角形 数学题目五边形里面有多少三角形 三人行教育网 Www 3rxing Org



五边形 维基百科 自由的百科全书


