球の半径から体積と表面積を計算します。 一部が欠けた球の体積 一部が欠けた球の体積 一部が欠けた球の体積と表面積を計算します。 弓形の回転体の体積 弓形の回転体の体積 弓形の回転体の体積と底面積と表面積を計算します。球冠,球帯の面積の求め方02 球をある平面で切り取った部分, 球冠 ,の表面積は,以下の図で示すように, 積分範囲を,0からl 2 までにすればよいので, と表すことができます. 4球体 球体の表面積の公式は下記の通りです。 球体の半径をrとし、円周率はπで表しています。 上記した球体の表面積の求め方の証明は、高校生で指導される積分が必要になります。そのため中学数学においては、記憶させるしかないと言えます。

中1 数学 中1 84 球について Youtube
球体 の 面積 の 求め 方 なぜ 4
球体 の 面積 の 求め 方 なぜ 4- よって,球帯の表面積は S = 2 π r 2 ∫ θ 1 θ 2 cos θ d θ S=2\pi r^2\int_{\theta_1}^{\theta_2}\cos\theta d\theta S = 2 π r 2 ∫ θ 1 θ 2 cos θ d θ (ただし, θ 1 \theta_1 θ 1 は球帯の底面の緯度, θ 2 \theta_2 θ 2 は球帯の天面の緯度) 球体 表面積 求め 方 球体 表面積 求め 方こんにちは!この記事をかいているKenだよ。豚肉を今日もいためたね。 球の表面積の求め方には公式があるんだ。 球の半径をrとすると、その表面積は、 4πr^2 になるよ。



水平投影面積とは 1分でわかる意味 計算法 法面
球の体積の求め方(公式)の次は、球の表面積の求め方(公式)を学習しましょう。 下の図のように、 半径rの球があるとき、球の表面積は、4πr2となります。 これもまた、球の表面積の公式がなぜ4πr 2 となるのか疑問に思う人もいるでしょう。最後に 球体の表面積 球体の表面積 目標:積分を用いて上式を導出する 方法を2つ考えました. 求め方1:微笑の範囲を考える方法 求め方2:球体の体積を用いる方法 求め方1:微小の範囲を考える方法 考え方 青い部分の面積 を考える.球の体積の求め方 公式と計算例 Scipursuit 体積の求め方 球 球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。 球の体積を求めるには、この公式に球の半径 r を代入すればよいだけです。 このページの続きでは、例題を使って、この公式の使い方を説明しています。
A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 最後に 球体の表面積 球体の表面積 目標:積分を用いて上式を導出する 方法を2つ考えました. 求め方1:微笑の範囲を考える方法 求め方2:球体の体積を用いる方法 求め方1:微小の範囲を考える方法 考え方 青い部分の面積 を考える.球の表面積を求める公式は、S = 4πr^2 で表 半径rの球の体積を求める公式は、次のようになります。 πは円周率 (=)です。 球の体積は、半径rの3乗に比例していくということですね!
小学6年生で習う、円の面積の問題の解き方を世界一やさしく解説します。 ★今から学ぶこと 1、円の面積を求める式円の面積=半径×半径×314 2、円の一部の面積を求める式円の面積の一部=半径×半径×314×中心の角/360° 3、色(かげ)がついた部分の面積の求め方全体白い部分ラブリー球体 表面積 求め 方 球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus 中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 今度は「球体の面積の求め方」を知りたくなりました。 (学校で使うので)誰でも良いので、よろしくお願いします。 球の面積は、4πr^2 です。



研究




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
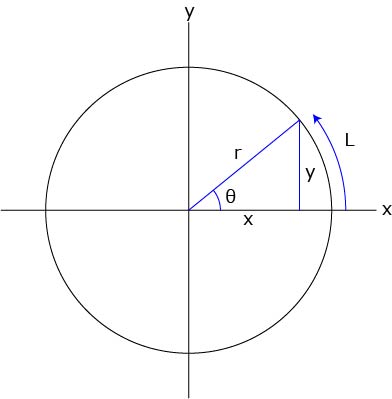
球の表面積 \(\pi D^2\) 球の体積 \(\left ( \displaystyle \frac {\pi}{6} \right ) D^3\) 球の質量 \(\left ( \displaystyle \frac {\pi}{6} \right ) D^3 \rho\) 球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) 球の質量基準比表面積(単位質量当たりの表面積) 目的 「楕円の面積」や「楕円体の体積」の求め方を紹介します。 理解のためのステップ ステップ ステップとして下記のステップを踏んで「4楕円体の体積」を求めたいと思います。 1円の面積 2楕円の面積 3球の体積球の体積と表面積 東京大学大学院数理科学研究科・教授 古田幹雄 1 円の面積と円周の長さ 半径rの円の面積はˇr2 です。 グラフv = ˇu2 のu = rにおける接線の傾きを求めてみま す。すると、答えは2ˇrとなります。これは半径rの円周の長さです。つまり、円の面積




球の表面積と体積の公式 数学fun




球の表面積と体積の公式 数学fun
球の体積、表面積の求め方例題 これにより n次元球体の体積が指数函数的に減少することの別証明が得られる( n が十分大きいとき、因子 R √ 2 π e/n は 1 より小さく、従って先ほどと同じ論法が適表面積 s S p h e r e ( 1 ) v o l u m e V = 4 3 π r 3 ( 2 ) s u r f a c e a r e a S = 4 π r 2 S p h e r e ( 1 ) v o l u m e V = 4 3 π r 3 ( 2 ) s u r f a c e a r e a S = 4 π r 2 空間中で球面の方程式を使う応用問題 <※この記事は、「球面の方程式の求め方の解説」を前提に解説していくので、まだ読んでいない方は、ぜひ先に上のリンクよりご覧ください。 2つの球が交わった時にできる円の方程式 さて、球面の方程式の応用問題で最も一般的なものから解いてい




球の表面積の公式について みたにっき はてな




Mathematics 球の体積と表面積を求める公式 働きアリ
体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱(管) 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方 うさぎでもわかる解析 Part27 2重積分の応用(体積・曲面積の求め方) こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめています。 前回の記事(Part26)はこちら! 広義積分・ガウス積分にHello School 算数 体積・表面積 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。




球の体積と表面積 公式と計算問題と証明 Irohabook




球体の表面積 積分で求める方法 うちーノート
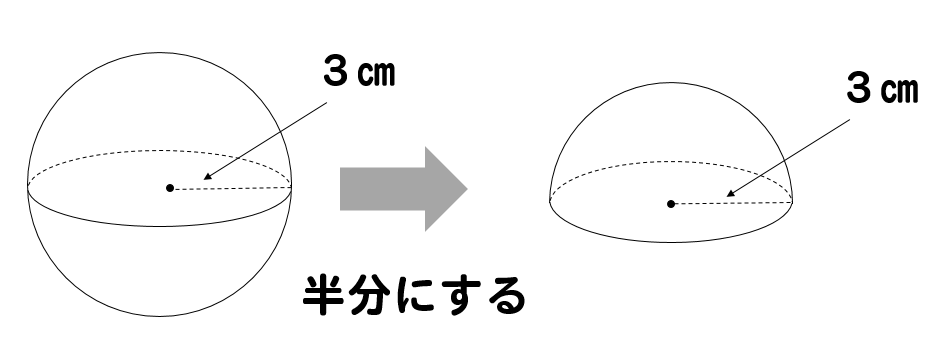
ドーム状の表面積の求め方を教えて下さい。 (球体の上一部の表面積の求め方です) また、その円周を求めるにはπr^2で Read 53 ①球の体積の公式の求め方 さてこの記事を読みに方は、楕円の面積や体積の公式を求めてきたことだと思います。 直径10センチの球面の方程式は x^2y^2z^2=25 x=0の面(YZ座標平面)で切断した切断面で考えると境界線は y^2z^2=25 の円周になる。 この端y=5からa(0≦a≦10 (センチ))の距離のy=5a (センチ)の平面(切断面では直線)で切断したときの切断面の直径Dは、D=2z=2√ (25y^2)にy=5aを代入して求めることが出来る。 D=2√ {25 (5a)^2}=2√ (10aa^2)(センチ) 半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求め




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
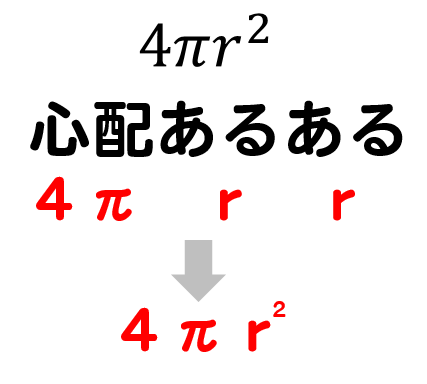
よって、球の体積Vは、円の面積をx 方向に積分すると、V=2∫0rπ(r2-x2) dxより、 V=2πr2x-(x3/3)0r=(4/3)πr3を導くことができる。 ②球の表面積の公式の求め方(1) 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4\pi r^2 4πr2 →「心配アール二乗」 球の体積: \dfrac {4} {3}\pi r^3 34 πr3 →「身の上に心配アール三乗」球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。



球冠の面積 Kfujitoの徒然 by浮沈子




球の体積と表面積 Youtube
円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!←今回の記事U = π (r 2 − h 2)※ 球の表面積は円の面積の4倍になる.(非常にきれいな関係) ※ 高校数学IIIで微分を習えば,体積 V= πr 3 を半径で微分すると表面積 S=4πr 2 になることが分かる.脱線ついでに言えば,円の面積 S=πr 2 を半径で微分すると円周の長さ L=2πr になる.




球の表面積 体積 身勝手な主張




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。優雅 球体 表面積 求め 方 壁紙 配布 球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館 Source pinterestcom元々球体の表面にある部分のk1とk2での表面積をs(k1)、s((k2)で表したとき、 s(k1) : s(k2) はどの様になるか? 完璧に球体であるリンゴを半分の半分としたリンゴのそれぞれの皮をむいたら、さてどちら の皮の面積がどれだけ大きくなるか想像してみよう。




円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ




球の体積 表面積の求め方 公式 小学生 中学生の勉強




中1 中1数学 球の体積と表面積 中学生 数学のノート Clear




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ



1



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



Sphere 01




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



学校で球の面積の求め方を 3分の2すると言われたのですが 調べ Yahoo 知恵袋




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ




球の表面積と体積の公式 数学fun




球帯の定理 感じる科学 味わう数学



1



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館




球体の表面積 中学生に分かるように真剣に考えてみた うちーノート
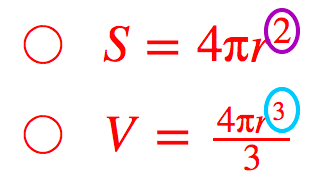



球の表面積と体積の求め方 苦手な数学を簡単に



数学 球の表面積を積分で計算してもうまくいかない人へ




球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




中学数学 回転体の体積 表面積を求める問題を解説するぞ 中学数学 理科の学習まとめサイト




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




中1 数学 中1 84 球について Youtube



立体 の 表面積 求め 方




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




半球の体積と表面積を計算する 具体例で学ぶ数学




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




球の表面積と体積の公式 数学fun
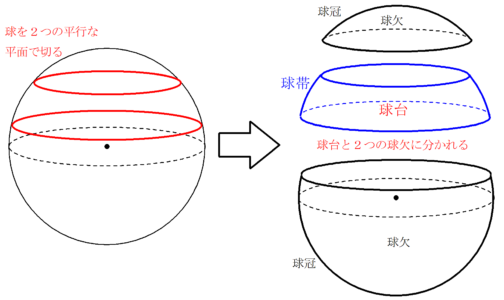



球台と球帯 Fukusukeの数学めも



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com



1
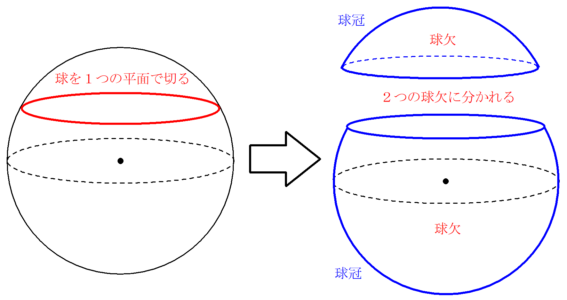



球欠と球冠 Fukusukeの数学めも




3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ




球体を切った時の直径の求め方 球体を切った時の直径の求め方を教えて 数学 教えて Goo



U9j580gf8iba369ji2w Xyz P 296




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




球体の表面積 中学生に分かるように真剣に考えてみた うちーノート




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



至急 球を4等分したものの体積と表面積の求め方をを教えてください Yahoo 知恵袋




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




球の表面積の公式について みたにっき はてな



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



大学入試問題




球の体積 球の表面積の公式の導出 積分 優技録




表面積の求め方 計算公式一覧



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス
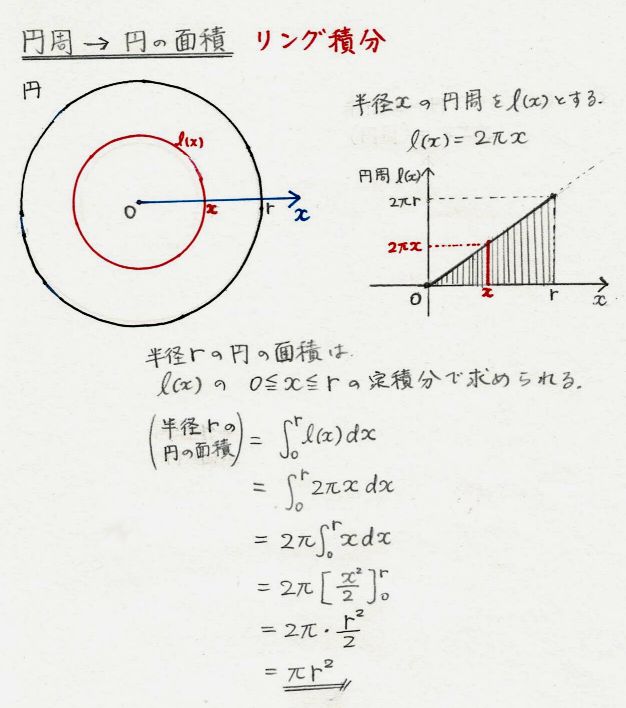



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



Sphere 01




中1 数学 6 5 球の体積 表面積 Youtube




球面積 球の體積 Juliech




球面三角形の面積の求め方 理数アラカルト




角錐 円錐の体積と表面積の公式 数学fun




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく
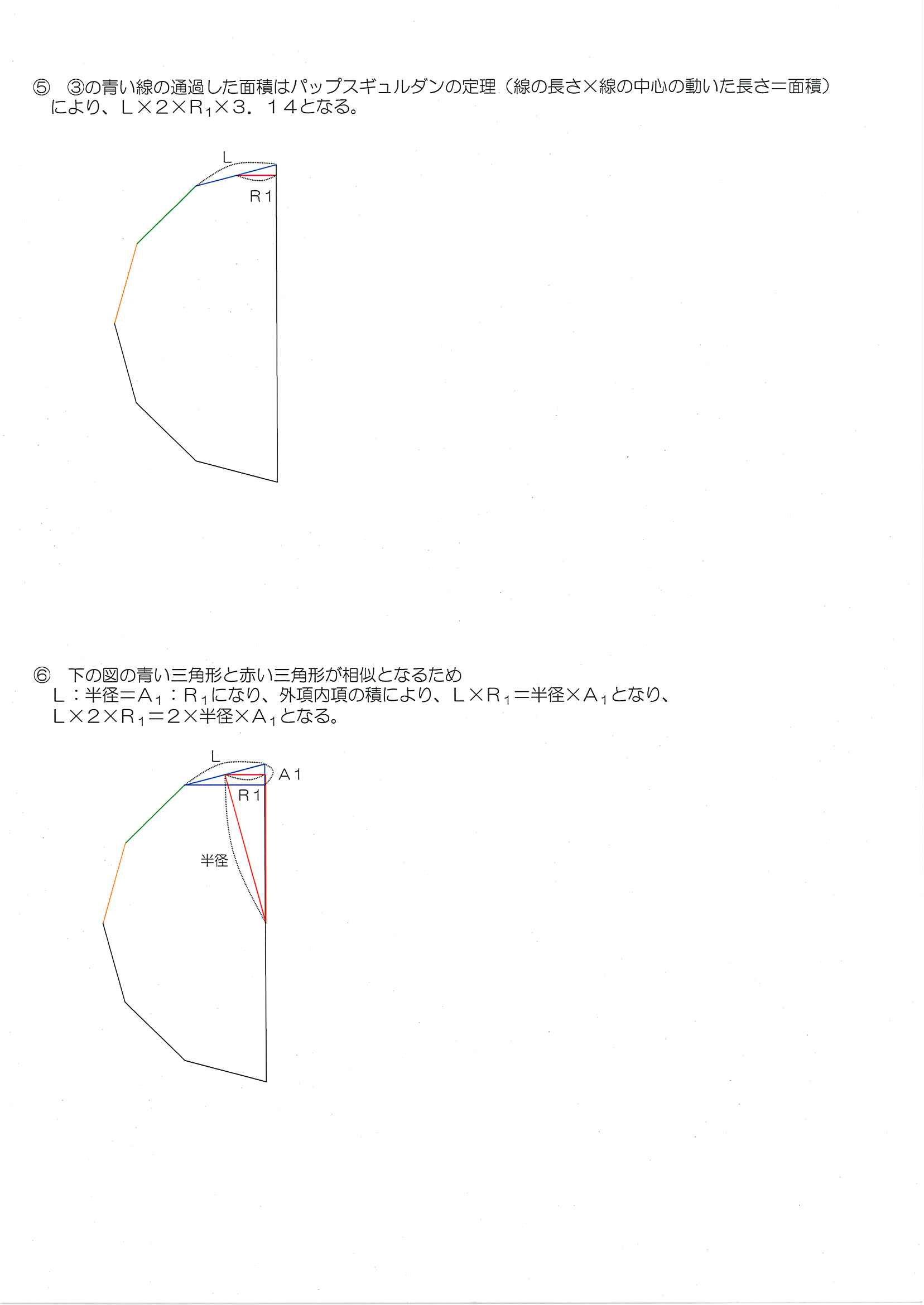



球の表面積の求め方 中学受験塾act アクト のブログ




球の表面積の求め方 その3 感じる科学 味わう数学



球の表面積の公式の求め方



水平投影面積とは 1分でわかる意味 計算法 法面




球の体積と表面積を積分で証明 高校数学の美しい物語



球の表面積と体積の求め方 苦手な数学を簡単に




初等幾何 球の表面積を求める 大人が学び直す数学




球の表面積と体積の公式 数学fun



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




球の表面積の求め方 公式と計算例




球の表面積を重積分を使って計算してみた Youtube




中1 中一数学 球の表面積と体積 中学生 数学のノート Clear




球の表面積 体積 身勝手な主張
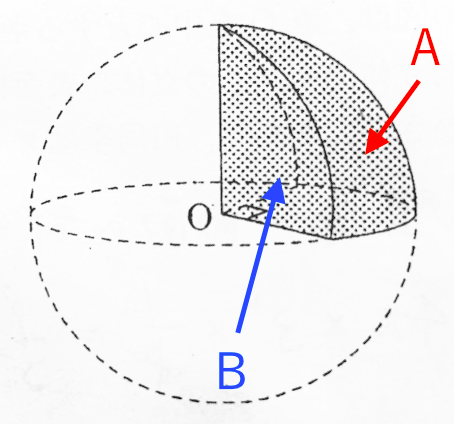



球の問題 苦手な数学を簡単に




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



1



球の表面積の公式の求め方




球の表面積と体積の公式 数学fun




球の表面積と体積の公式 数学fun



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



Fhpxqjuuu3lszm




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積の求め方でなぜ3分の4が出てくるのかわかりません 中1でもわかるように説明お Clear




球の体積公式の微分が表面積になっている理由 Youtube




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく


